OpenRE devlog 3 : Harmonisation des normales

Table des matières

⬅️ Vers Précédent : “OpenRE devlog 2 : Harmonisation de la profondeur”

I. Introduction

Si vous êtes un lecteur du futur et que vous lisez ces develogs d’une traite, vous avez sûrement la structure des précédents numéros en tête. Mais si vous les découvrez au fur et à mesure, un petit rappel me semble approprié.

Depuis le début de cette série, nous avons entrepris d’harmoniser les différents jeux de textures issus de Blender et Godot qui composent nos G-Buffers déterministes et interactifs. Jusqu’ici, nous avons traité :

  • l’albédo
  • la profondeur

Pour nous aider dans cette tâche, nous avons mis au point un petit outil que nous appelons “l’Oracle” et qui nous permet de comparer les textures deux à deux. Le résultat de la comparaison prend la forme d’une image (que nous appelons “prophétie”) dans laquelle chaque pixel représente le degré de différence mesuré entre les deux textures sources. Il s’interprète comme ceci :

  • pixel blanc : La différecne est maximale
  • pixel noir : les sources sont identiques

Aujourd’hui, nous allons nous occuper des textures de normales. Et comme à chaque fois, il y aura :

  • une première partie expliquant comment obtenir les textures avec les deux logiciels
  • une seconde partie présentant les ajustements effectués pour avoir des textures bien en phase

II. Génération des textures

Une fois n’est pas coutume, nous allons utiliser une nouvelle passe Cycles dédiée côté déterministe, et une Render target avec un post-process côté interactif.

1. Normale interactive

Commençons tout de suite avec le post-process. Cette fois, la texture qui nous intéresse est la hint_normal_roughness_texture. Voici le code complet :

shader_type spatial;
render_mode unshaded, fog_disabled;

uniform sampler2D depth_texture : hint_normal_roughness_texture, repeat_disable, filter_nearest;

void vertex() {
	POSITION = vec4(VERTEX.xy, 1.0, 1.0);
}

void fragment() {
	vec3 normal = texture(normal_roughness_texture, SCREEN_UV.xy).xyz;
	ALBEDO = normal;
}

Rien de particulier ici. On ignore simplement la roughness stockée dans le composant w de la hint_normal_roughness_texture parce qu’on n’en a pas besoin.

2. Normale déterministe

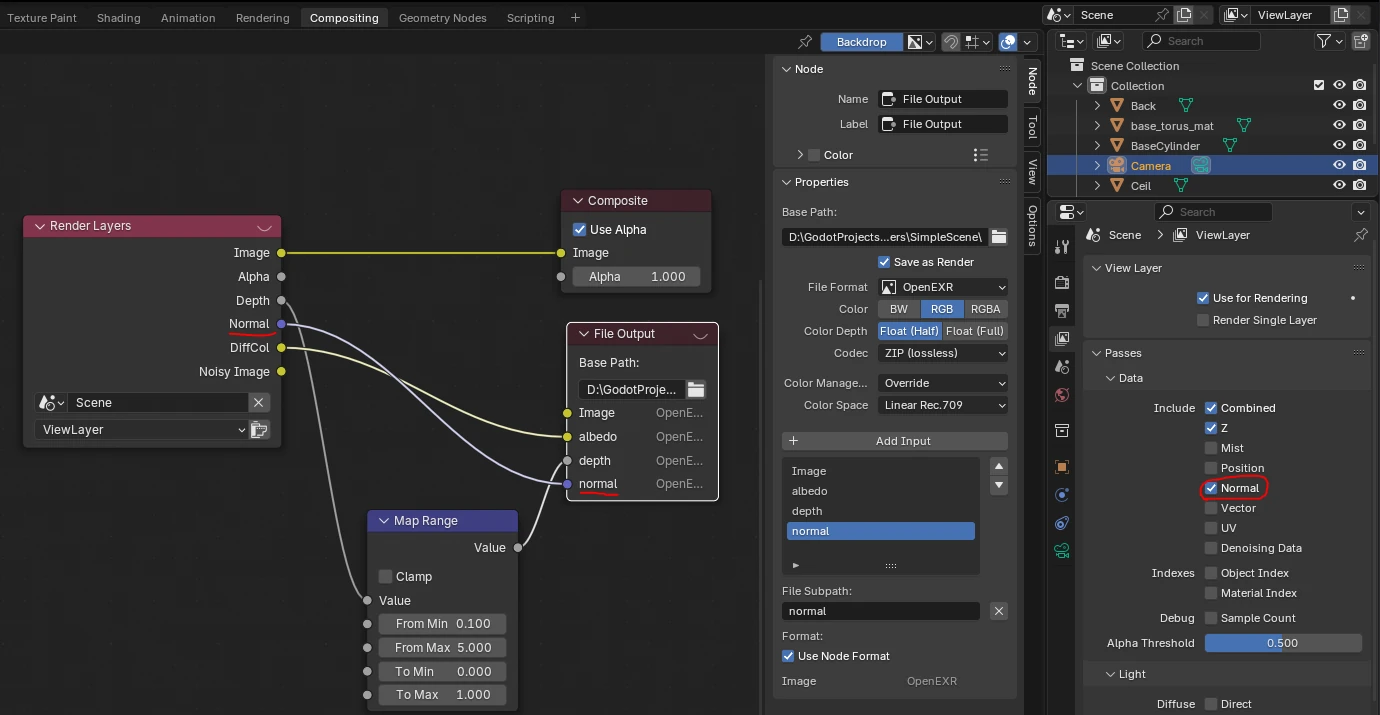
La passe à activer est ici assez évidente. Elle s’appelle tout simplement : Normal. Vous commencez surement à être familier avec le procéssus :

  • On active la passe Normal depuis le panneau latéral
  • On ajoute un pin normal au nœud File Output du Compositor
  • On relie les deux et on appuie sur F12 pour générer le rendu

Capture d’écran montrant comment activer la normal pass de Cycles

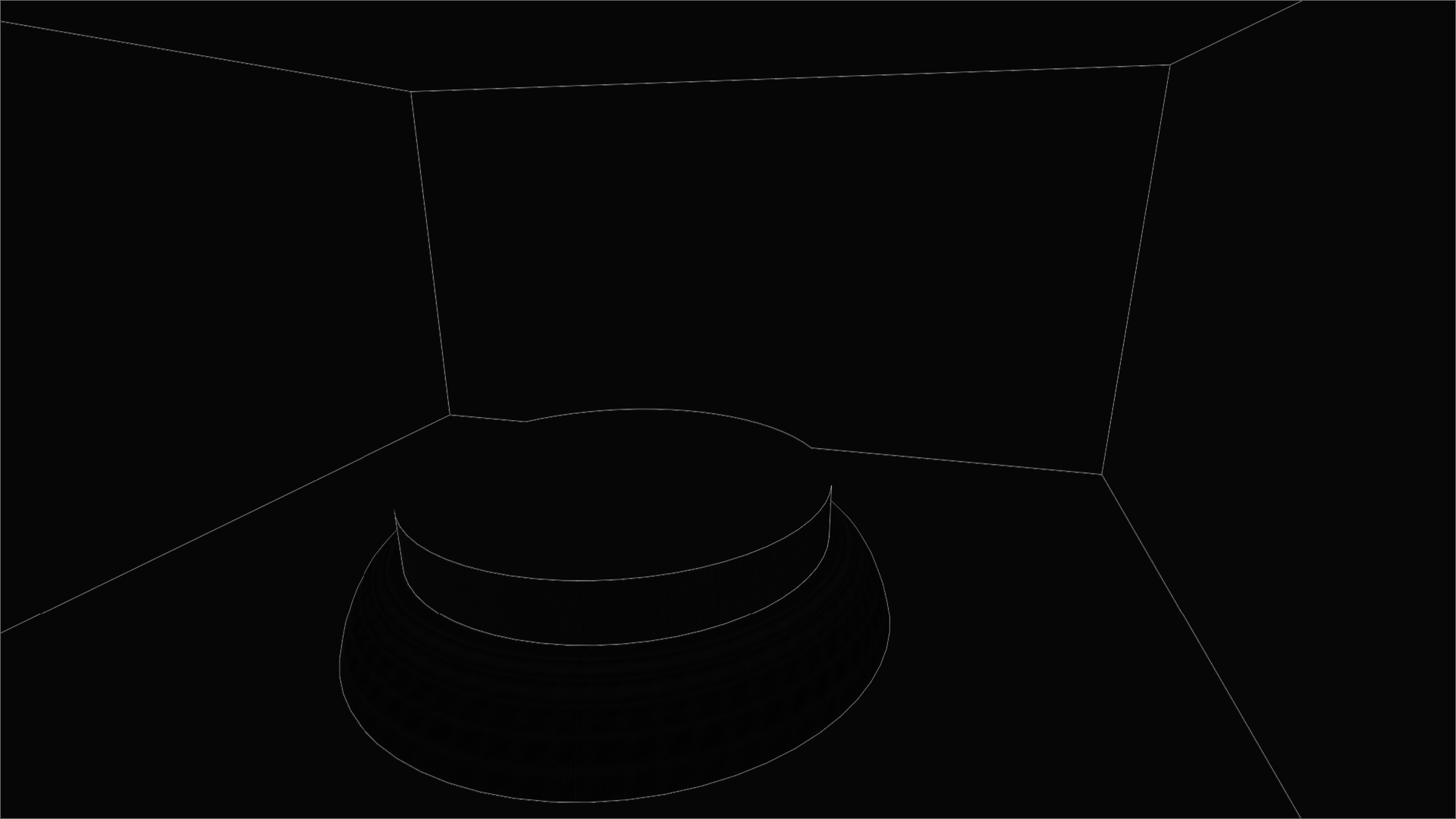
À ma grande surprise, l’image obtenue ressemble à ça :

Capture montrant le resultat buggé de l’export de la normal pass de blender

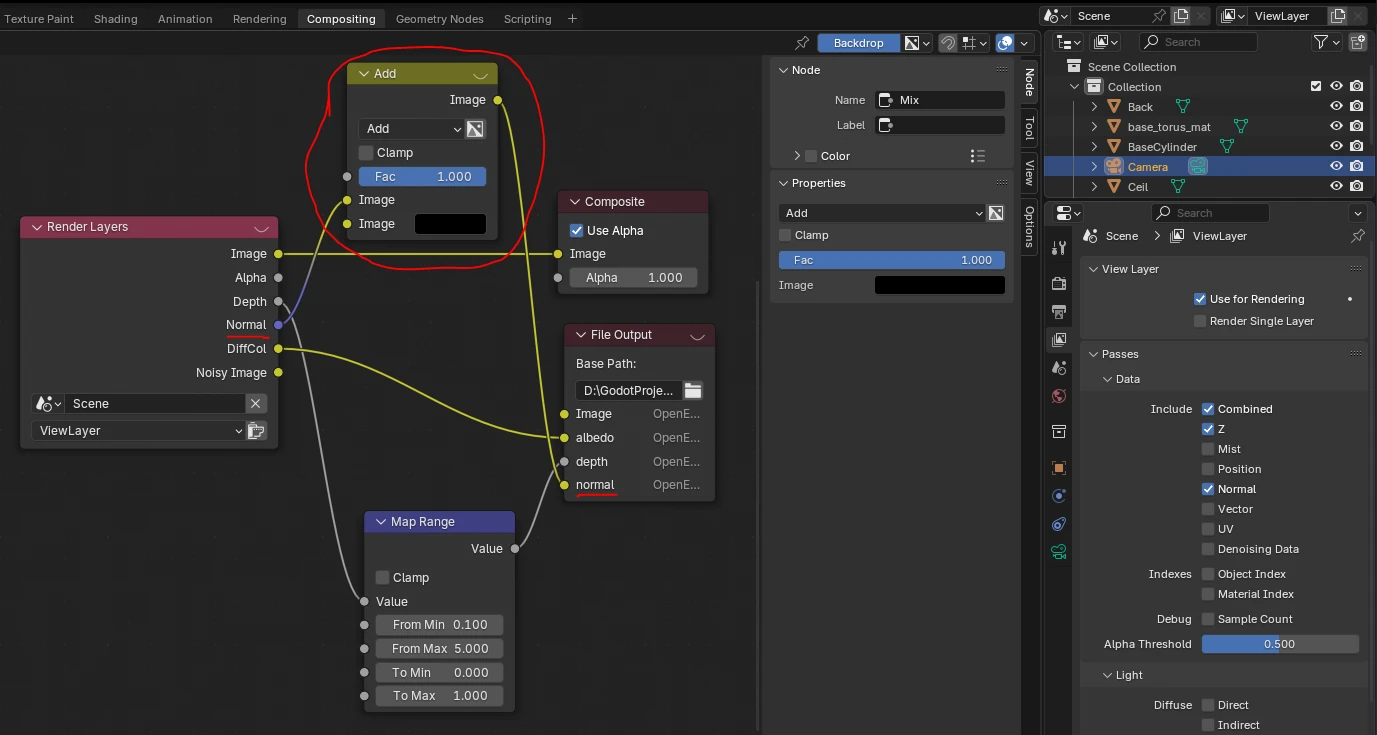
Ce n’est évidemment pas ce qu’on veut. Je pense qu’il s’agit d’un bug de Blender, car le contournement est pour le moins suspect :

Capture d’écran montrant comment fixer le bug d’export de la normal pass

Il suffit d’ajouter un nœud qui ne fait rien du tout entre les deux pins. Par exemple, le nœud Add dans l’illustration ci-dessus qui ajoute à la normale la couleur noire (0, 0, 0). Lorsqu’on fait ça, le rendu redevient cohérent :

Capture montrant la normal pass fixée

III. Réglages

Cette fois encore, il a fallu modifier l’oracle pour qu’il supporte la comparaison des textures de normales. Sans entrer dans les détails, j’ai ajouté une fonction de prétraitement pour chacune des textures :

vec3 pre_process_i_normal(vec3 i_normal) {
	return i_normal;
}

vec3 pre_process_d_normal(vec3 d_normal) {
	return d_normal;
}

Notez également que nous allons traiter des directions. On va donc changer notre critère de comparaison habituel (distance euclidienne) et utiliser quelque chose de plus pertinent dans ce contexte : l’angle entre les vecteurs (que l’on projettera sur [0, 1] en le divisant par π).

vec3 compute_normal_difference(vec3 d_frag, vec3 i_frag) {
	float angle = acos(dot(d_frag, i_frag)) / PI;
	return vec3(angle, angle, angle);
}

1. Normal Packing / Unpacking

Si on compare les textures en l’état, on remarque que les couleurs sont très différentes, mais pas seulement. Si on observe la texture déterministe, on constate aussi que :

  • certaines faces sont noires
  • les faces opposées à une face noire sont systématiquement colorées

Comparaison côte à côte des textures de normales interactive et déterministe

Quand on y réfléchit, c’est parfaitement normal car, contrairement à une couleur, un vecteur peut avoir des composantes négatives. Lorsqu’on essaie de les visualiser, ces dernières sont clampées à 0, et un vecteur n’ayant que des valeurs négatives apparaît donc noir.

Non seulement ce n’est pas pratique pour la visualisation, mais surtout la plupart des formats d’images ne permettent pas d’encoder des valeurs négatives. Ici ce n’est pas le cas car on utilise EXR, mais avec un autre format, les valeurs seraient clampées à l’export et la donnée serait tout simplement perdue.

La solution usuelle à ce problème est de projeter les composantes des normales de l’intervalle [-1, 1] vers l’intervalle [0, 1] avant d’exporter. On appelle ce procédé le “normal packing”. Par la suite, pour retrouver nos normales et faire nos calculs dans le shader après import, il suffit d’effectuer l’opération inverse (“normal unpacking”).

// ... Normal generation ...

vec3 packed_normal = (normal + 1.0) / 2.0;

// ... Export ...

// ... Import ...

vec3 unpacked_normal = packed_normal * 2.0 - 1.0;

// ... Shader computations ...

Nous avons donc une texture déterministe “unpacked” et une texture interactive “packed”. Ce qui nous arrangerait, ce serait que les deux soient “packed” pour la visualisation et “unpacked” pour le calcul de différence. Nous allons donc packer la texture déterministe dans pre_process_d_normal :

vec3 pre_process_d_normal(vec3 d_normal) {
	return (d_normal + 1.0) / 2.0;	// Pack
}

Et dépacker les deux avant le calcul de différence dans compute_normal_difference :

vec3 compute_normal_difference(vec3 d_frag, vec3 i_frag) {
	d_frag = d_frag * 2.0 - 1.0;	// Unpack (previously packed in pre_process_d_normal())
	i_frag = i_frag * 2.0 - 1.0;	// Unpack
	
	float angle = acos(dot(d_frag, i_frag)) / PI;
	return vec3(angle, angle, angle);
}

Les couleurs sont toujours aux fraises, mais on a fait un premier pas. Et surtout, on peut maintenant visualiser correctement la texture déterministe sans avoir à deviner ce qu’il se passe dans les zones noires.

Comparaison côte à côte des textures de normales interactive et déterministe (packée)

2. View vs World

Une question qu’il faut toujours se poser quand on écrit un shader, c’est : “dans quel espace sont exprimées mes données”. En effet, il y a deux écoles :

  • faire les calculs en VIEW_SPACE (l’espace de la caméra)
  • faire les calculs en WORLD_SPACE (l’espace de la scène)

Les deux options sont parfaitement viables, mais évidemment, il faut choisir et s’assurer que toutes les données soient bien conformes à ce choix (et les changer d’espace si ce n’est pas le cas). Il est donc primordial de savoir dans quel espace Blender et Godot expriment leurs normales.

J’ai été surpris de ne pas trouver l’info dans leurs documentations respectives. Mais heureusement, ce n’est pas très difficile à déterminer. Il suffit de faire varier l’angle de la caméra et d’observer les couleurs qui représentent les normales.

  • Si les couleurs varient avec l’angle, on est en VIEW_SPACE
  • Si les couleurs ne bougent pas, on est en WORLD_SPACE

Il se trouve que Blender est en WORLD_SPACE et Godot en VIEW_SPACE. Je préfère travailler en WORLD_SPACE. On va donc utiliser pre_process_i_normal pour effectuer le changement d’espace côté Godot :

vec3 pre_process_i_normal(vec3 i_normal, mat4 inv_view_matrix) {	
	i_normal = i_normal * 2.0 - 1.0;	// Unpack for space switch
	i_normal = (inv_view_matrix * vec4(i_normal, 0.0)).xyz;
	return (i_normal + 1.0) / 2.0;		// Repack for visualisation
}

Vous noterez qu’on effectue un “unpacking” avant le changement d’espace, ce qui est normal. Mais il ne faut pas oublier de “repack” juste après pour pouvoir visualiser la texture correctement.

Par ailleurs, si vous vous demandez comment on obtient le paramètre inv_view_matrix qui nous permet de changer d’espace, c’est très simple. Godot expose à ses shaders la matrice INV_VIEW_MATRIX. Mais elle n’est accessible que depuis void fragment() (le main du fragment shader dans le langage de shading de Godot). Il faut donc la passer en paramètre.

Observons maintenant la différence entre les deux espaces :

Comparaison animée des textures déterministes en world space et view space

Elle est visible mais pas très prononcée. Cela s’explique par le fait que notre caméra est presque alignée avec le repère. Dans ce cas, VIEW_SPACE et WORLD_SPACE sont très proches l’un de l’autre vis-à-vis de la rotation. Cela aurait été beaucoup plus flagrant si la caméra regardait dans une autre direction. D’où l’importance d’avoir à terme plusieurs scènes de test car sans s’en rendre compte, on peut très vite se placer dans des cas particuliers.

3. Permutations du repère

Évidemment, Blender et Godot n’utilisent pas le même repère. Le “up vector” de Godot est l’axe Y, alors que celui de Blender est l’axe Z. C’est la raison pour laquelle les couleurs représentant les normales ne matchent pas : les canaux sont en quelque sorte inversés. Il faut donc réorganiser tout ça dans pre_process_d_normal. En comparant les gizmos des deux logiciels, je suis arrivé à la conclusion que la bonne permutation était la suivante :

Illustration montrant les repères des 2 logiciels de part et d'autre d'un flêche horizontal annotée '(x, y, z) => (x, z, -y) ?'
vec3 pre_process_d_normal(vec3 d_normal) {
	d_normal = vec3(d_normal.x, d_normal.z, -d_normal.y);	// Permut
	return (d_normal + 1.0) / 2.0;							// Pack
}

Malheureusement, l’Oracle n’avait pas l’air d’accord. En effet, sur la prophétie, on peut voir que le sol et le mur gauche de la cornell-box ne sont pas noirs, indiquant que les vecteurs up et right ne sont pas en phase.

1er prophecie de l’oracle. Le mur gauche ainsi que le sol sont trè claires

Ma vie étant visiblement un mensonge, j’ai essayé d’autres permutations un peu au hasard. Vous savez, ce moment où l’on ne comprend pas son erreur et où l’on commence à changer un signe par-ci, inverser des termes par-là… (je sens d’ici les regards désapprobateurs, mais je sais que vous le faites aussi 😅).

Comme souvent, cela ne m’a pas mené bien loin. Mais cela ne veut pas dire que le “random programming” soit mauvais en soi. Il faut juste le faire bien, c’est-à-dire guider par un raisonnement et non par la flemme.

Il n’y a que 48 permutations possibles. Ce n’est pas la mer à boire. Si je suis capable de reconnaître la bonne à coup sûr, j’ai juste besoin d’une moulinette pour itérer rapidement sur toutes les entrées. Cette moulinette, la voici :

// Applique une permutation parmis les 48 possible
vec3 _dbg_normal_permut(vec3 normal_src, int permut_idx) {
	switch(permut_idx) {
		case 0 : return vec3(normal_src.x, normal_src.y, normal_src.z);
		case 1: return vec3(normal_src.y, normal_src.z, normal_src.x);
		case 2: return vec3(normal_src.z, normal_src.x, normal_src.y);
		case 3: return vec3(normal_src.z, normal_src.y, normal_src.x);
		case 4: return vec3(normal_src.y, normal_src.x, normal_src.z);
		case 5: return vec3(normal_src.x, normal_src.z, normal_src.y);
		
		// ...
		
		case 42: return vec3(-normal_src.x, -normal_src.y, -normal_src.z);
		case 43: return vec3(-normal_src.y, -normal_src.z, -normal_src.x);
		case 44: return vec3(-normal_src.z, -normal_src.x, -normal_src.y);
		case 45: return vec3(-normal_src.z, -normal_src.y, -normal_src.x);
		case 46: return vec3(-normal_src.y, -normal_src.x, -normal_src.z);
		case 47: return vec3(-normal_src.x, -normal_src.z, -normal_src.y);
	}
}

// Uniform permetant de selectionner la permutation au runtime
uniform int dbg_permut_idx = 0;

vec3 pre_process_d_normal(vec3 d_normal) {
	// Application de la permutation selectionnée
	d_normal = _dbg_normal_permut(d_normal, dbg_permut_idx);
	return (d_normal + 1.0) / 2.0;		// Pack
}

À partir de là, il suffit de faire play, de régler le visualisation_mode de l’oracle sur D_TEXTURE_ONLY et d’incrémenter dbg_permut_idx dans l’éditeur jusqu’à ce que l’image soit noire.

Capture d’écran montrant comment fixer le bug d’export de la normal pass

Bon, d’accord, l’image 11 n’est pas complètement noire, mais elle sort quand même bien du lot :

  • Elle est globalement plus sombre.
  • C’est la seule à n’avoir aucune face complètement blanche.
  • Elle ressemble quand même beaucoup à la première permutation que nous avons essayée… C’est quoi la formule ?…
// Applique une permutation parmis les 48 possible
vec3 _dbg_normal_permut(vec3 normal_src, int permut_idx) {
	switch(permut_idx) {
		// ...
		
		case 11: return vec3(normal_src.x, normal_src.z, -normal_src.y);

		// ...
	}
}

Ok… c’est exactement la même en fait… Maintenant qu’on a comparé l’entrée avec toutes les autres, ça paraît évident : on était bons depuis le début. Le problème ne venait pas d’une erreur de permutation des axes. C’était autre chose.

4. Normalisation

J’ai mis un certain temps à résoudre l’énigme. J’ai même envisagé l’idée de ressortir la carte “Good Enough”. Après tout, le présage n’est pas bien pire que celui qu’on avait accepté pour l’albédo, et quand on compare les textures actuelles, ils est quasi impossible de les distinguer.

Comparaison animée des textures interactive et déterministe en l’état

Mais dans le cas des normales, on ne peut pas se contenter d’un jugement à l’œil. On les représente par des couleurs pour pouvoir les visualiser facilement, mais il faut garder à l’esprit que ce sont en réalité des données mathématiques qui interviennent dans des calculs complexes. Le risque d’accumuler de l’erreur au fil des opérations est trop grand. Il faut faire mieux !

Le souci était en fait tout bête. Pour calculer l’angle entre les vecteurs dans compute_normal_difference la formule devrait être :

float angle = acos(dot(v1, v2)) / (length(v1) * length(v2));

Mais dans notre cas, les vecteurs sont des normales. Leur norme est donc en principe égale à 1. Le dénominateur peut donc être ignoré, c’est pourquoi j’utilise la version simplifiée :

float angle = acos(dot(v1, v2));

J’ignore pourquoi, mais il s’avère que les normales fournies par Blender et Godot ne sont pas toujours de norme 1. Pour le mettre en évidence, j’ai temporairement modifié les fonctions pre_process_i_normal et pre_process_d_normal afin que l’on puisse visualiser l’erreur grossie 100 fois.

vec3 pre_process_i_normal(vec3 i_normal, mat4 inv_view_matrix) {
	i_normal = i_normal * 2.0 - 1.0;	// Unpack
	float norm_err = (1.0 - length(i_normal)) * 100.0;
	return vec3(norm_err, norm_err, norm_err);
}

vec3 pre_process_d_normal(vec3 d_normal) {	
	float norm_err = (1.0 - length(d_normal)) * 100.0;
	return vec3(norm_err, norm_err, norm_err);
}

Le résultat est sans appel. Dans un cas comme dans l’autre, les normales ne sont pas toujours unitaires :

Comparaison côte à côte des erreures de taille de normal grossies 100x. A gauche, blender est mauvais principalement sur les angles. A droite godot est bruité sur les surface courbe et sur les murs de gauche et le sol produites

Si l’on normalise les vecteurs avant le calcul de l’angle, on obtient un résultat de bien meilleure qualité :

vec3 compute_normal_difference(vec3 d_frag, vec3 i_frag) {
	d_frag = d_frag * 2.0 - 1.0;	// Unpack
	i_frag = i_frag * 2.0 - 1.0;	// Unpack
	
	d_frag = normalize(d_frag);		// Fix norm err
	i_frag = normalize(i_frag);		// Fix norm err
	
	float angle = acos(dot(d_frag, i_frag)) / PI;
	return vec3(angle, angle, angle);
}

2nd prophecie de l’oracle. Tout est bien noir à l’exception des contours. On voit apparaitre de légers paternes semblant suivre la géométrie des faces sur les surfaces courbes

On notera la présence de motifs sur les surfaces courbes. Les motifs semblent suivre les face qui composent la géométrie du mesh. Je pense que ça vient de la façon dont les deux logiciels calculent les normales des vertex. C’est toujours plus ou moins une moyenne des normales des faces adjacentes, mais il existe plusieurs heuristiques pour pondérer cette moyenne (prorata des surfaces, des angles, mix des deux, etc.). Godot et Blender n’utilisent certainement pas la même, mais ce ne sera pas un problème pour nous. Si notre bottleneck est l’heuristique choisie, on peut s’arrêter là. On est bien assez précis.

IV. Conclusion

L’harmonisation des normales aura été plutôt facile. Mis à part le coup des normes non unitaires et le possible bug de Blender, je m’attendais à peu près à tous les réglages effectués. Les questions d’espace, de repère ainsi que ces histoires de packing sont en effet assez usuelles en programmation graphique. Ce sont des pièges auxquels on finit par penser naturellement après être tombé dedans 10 fois.

Nous disposons donc désormais d’une calibration satisfaisante de Blender et Godot pour les maps suivantes :

  • albédo
  • depth
  • normales

Ce sont les données minimales nécessaires à une première implémentation de la lumière. On va donc pouvoir laisser l’Oracle un peu tranquille et commencer à intégrer de vrais éléments interactifs par-dessus un arrière-plan déterministe et voir comment on gère l’illumination dans les deux sens.

C’est donc dans le prochain numéro que les pièces vont enfin commencer à s’assembler. J’ai hâte de trouver un peu de temps pour m’y atteler… alors à très vite, je l’espère !

comments powered by Disqus